Lazy Portfolios 3 – One Fund from Vanguard

Today’s post is the third in a series of posts about of Lazy Portfolios. We’ll be looking at single fund solutions from Vanguard.

My portfolio

Let’s start with a quick recap of what we’ve covered so far.

My base portfolio is a passive global multi-asset portfolio made mostly from low-cost ETFs.

• I use 54 asset classes with an allocation based around volatility parity.

A true volatility parity portfolio is quite safe (and low return), with more than 60% in bonds.

• In order to hit my target / fail safe withdrawal rate of more than 3% pa, I need to cap the bond allocation to 20% – this allows for 75% stocks and 5% True Alternatives.

I also tweak the default allocation to accommodate global ITs and themed funds, and to support some home bias.

Lazy portfolios

Lazy portfolios are pretty much at the opposite end of the spectrum.

• Typically they involve between two and four funds, though some have more.

Their key advantage is simplicity.

• This doesn’t matter much to me – I don’t see the big difference between buying four ETFs and a dozen, or even 50.

But novice investors and those with small portfolios might find them useful.

Common portfolios

Returns are broadly proportional to volatility.

• In order to get good returns, you need to accept more volatility.

So correlations between assets – and in particular, correlations with the primary return-producing asset, stocks – are key.

• Adding poorly correlated assets can reduce the volatility of a portfolio without significantly affecting returns.

This leads to three common portfolios:

1. The Max SR portfolio (volatility optimised)
   • We’ll simplify this to be 60% bonds, 40% stocks.
2. The Max Return portfolio, which is 80% stocks and 20% bonds
   • I swap 5% of stocks for True Alternatives, to leave me with 75% stocks
3. A Compromise portfolio suitable for a wide range of people,
   • This might be 60% stocks, 35% bonds and 5% Alternatives.

Benchmark

We need something along the same lines as my “max return volatility parity” portfolio, but with fewer funds.

• Then we can compare the lazy allocations to our simplified portfolios.

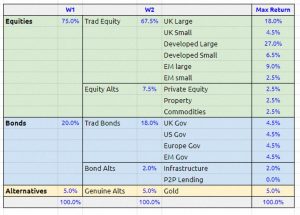
The best I could come up with was a 15-fund portfolio.

• There are six equity funds, three equity alts, four bonds funds, one bond alt and just one true alternative asset – gold.

This chart adds two more benchmarks:

• The Max SR benchmark, and
• The Compromised benchmark.

They have been derived from the max return benchmark by varying the allocations to stocks and bonds.

• Note that the two new benchmarks each include 16 funds rather than 15.

The idea is that we will compare each lazy portfolio to the three benchmarks in order to discover which type of investor it serves best (unless that is immediately obvious).

---

Note that it isn’t possible to produce high and stable returns from a static portfolio under all economic conditions conditions.

• Long-term investors should stick with stocks as the core of their portfolio, using diversifiers (bonds and true alternatives) to smooth their path a little.

So we will be measuring the lazy portfolios on how well they perform this task.

One fund portfolios

The only one-fund portfolios I come across in the UK are the Vanguard LifeStrategy funds.

• This is a series of fairly cheap (0.22% pa) index funds (not ETFs) that maintain a set allocation between global equities and global bonds.

The range of five funds runs from 20% stocks to 100% stocks, in steps of 20%.

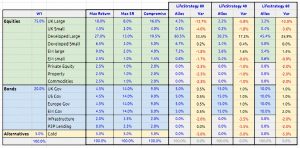
• The three that match most closely to our three benchmark portfolios are the 40%, 60% and 80% equity funds.

Transparency

Vanguard don’t make it particularly easy to work out what’s inside the fund (beyond the headline allocation).

• They use their own benchmarks, and
• They fill the fund with other funds from Vanguard.

The table above shows the allocations for the 40% stocks fund.

---

So we’ll need to make some assumptions.

• My plan is to make benevolent assumptions that bring the allocations as close to our benchmarks as is reasonable.

The only area where this might not be the case is home bias.

• I’ve seen discussions on bulletin boards to the effect that that the LifeStrategy series has a “harmful” home bias to the UK.

I can’t easily find the evidence for this, so I will assume a global market cap allocation.

• Of course, since I approve of some home bias, this actually works against the funds.

The numbers

The allocations I’ve used are:

• UK = 6%
• EMs = 10%
• Developed = 84%
• Small cap = 10% of each market

I’ve split bonds equally by region to match our benchmarks.

Here’s how those assumptions work out:

Relative to the appropriate benchmark:

• UK stocks are low
• Developed stocks are high
• EM is mixed – low for LifeStrategy 80, high for the other two.
• Bonds are a bit high but not too bad.
• There are no alternatives of any kind.

One number

In order to compare these variances with those of all the other lazy portfolios from future articles, we need to come up with some metrics, which can ideally be reduced to a single number.

I use three measures when comparing the asset allocation in my passive portfolio with my target allocation:

1. I average the variances across 17 “super-categories” of the 37 assets in the portfolio
2. I produce an absolute average for the same 17 variances (by ignoring whether the variance is positive or negative)
3. And I look at the standard deviation of the variances.

I then convert these three numbers into one by taking the geometric mean of them.

• I don’t claim that this mean has any statistical significance – it’s just a “speedometer” to let me track when my portfolio is drifting too far from it’s target allocation.

---

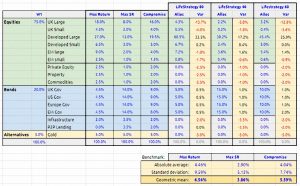
When I calculate these numbers for the Vanguard funds, the first two are identical.

• I think this is because the allocations sum to 100%, whereas my passive portfolio often has cash to be allocated or funds to be sold, and doesn’t match its target value.

So we’ll drop one of the averages and calculate the geometric mean of the remaining two numbers.

So what do these numbers mean?

• From my perspective, they look horrific.

I use 17 categories, and these benchmarks have 16 funds, so the numbers should be comparable with the ones I see everyday.

• For my own portfolio, I get twitchy when the geometric mean gets up towards 1.5%.
• I don’t start to relax until it’s below 1%, and ideally less than 0.5%.

Dropping the smallest of the three numbers to match the treatment of the Vanguard funds converts these thresholds to approximately 2.4%, 1.5% and 0.8%.

• So there’s no way I could live with these errors of 3.7% to 6.5%.

I’ve proved to my own satisfaction that the Vanguard funds don’t make suitable portfolios.

• And I think it will be interesting to see how the other lazy portfolios shape up.

I’m hoping that some of them will have errors below 2%, ideally against the Max return benchmark.

---

That’s it for today.

• In the next article we’ll look at some two fund portfolios.

Until next time.