ERN’s Options Strategy

Today’s post is the first in a new series on options trading. We’ll start with a look at a trading strategy from ERN, our go-to guy on Safe Withdrawal Rates.

Skew

We’ve previously looked at the idea that investors like positive skew, and will overpay for it.

• This means that you can make money by selling insurance and/or lottery tickets.

In practice, lottery tickets are harder for an individual to sell, and so the best strategy is simply to avoid buying them (and the financial assets – particularly blue-sky / long-shot stocks – which resemble them.

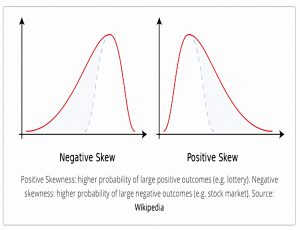
Here’s the Wikipedia diagram for skew.

• Positive skew means more chance of a large positive outcome (a lottery win).
  • Your downside is capped to the price of the lottery ticket.
• Negative skew means more chance of a large negative outcome (the stock market in general).

Note that this doesn’t say anything about average (expected) returns – the stock market return is usually positive.

• Those charts don’t show where the horizontal zero is.

ERN’s options strategy is a form of selling insurance.

• He has written six articles about options trading and also given an interview on the topic.

So I don’t expect to get through everything in one go today – but let’s get started.

ERN

ERN is the guy who runs the Early Retirement Now blog.

• ERN is not his real name, but he wrote anonymously for a few years and so it became his nickname.

We’ve looked at a lot of ERN’s posts before – specifically his mammoth series on safe withdrawal rates.

ERN is one of my favourite financial bloggers, for a number of reasons:

1. He looks in detail at subjects that other bloggers tend to skip over.
2. He has a practical approach because he usually plans to invest his money in the strategies he is testing.
3. He’s an ex-finance professional with a solid maths background.

He’s also a pretty engaging writer.

---

One of the other big topics on ERNs website – which might surprise some of the SWR fans –  is options trading.

• ERN has a lot of money tied up in options.

Specifically, he sells out-of-the-money short-dated put options to take advantage of other investors’ willingness to overpay for strategies with a positive skew.

Options

People like positive skew for evolutionary reasons.

• For most of history, one big negative result (illness, being eaten by a tiger) was the end of you.

This means that people like to protect their downside equity risk, perhaps by buying index put options.

• Which means in turn that buying these options is expensive, and buying them consistently is a losing strategy.

Flip this around, and selling this downside protection (selling put options) is profitable.

• But this approach has four times the negative skew of the regular stock market.

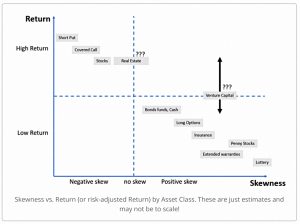
ERN drew his own chart of returns versus skew, and there’s a decent trend line in there.

The upside of skew

ERN has two “tricks” to convince himself that negative skew is a good thing (apart from the fact that things with negative skew often have good expected returns).

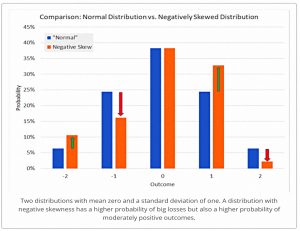
The first is that negative skew distributions have higher probabilities of positive outcomes, as shown in the chart above.

• The orange column is higher at -2, so has to be lower at -1 and +1 (otherwise the mean and variance would change).

ERN notes that 94% of his options trades are profitable, even though most of them run for less than a week.

• And 85% of daily returns are positive, which makes the occasional large loss easier to deal with.

---

The second is that skewness is less of a problem when you average over many trades – this is known as time diversification.

• The daily skew of ERN’s option portfolio is -5.1 (compared to minus 0.5 for the S&P 500)
• The weekly skew is -4.9
• The monthly skew is -1.9, and
• The quarterly skew is +0.1

ERN explains this is because of the Central Limit Theorem:

The average outcome from independent draws from even very non-Normal distributions (e.g. very negatively skewed distributions) will look more and more “Normal” and thus unskewed.

Expected returns

Antti Ilmanen of Expected Returns fame also has a paper on insurance and lottery tickets.

Selling insurance and selling lottery tickets have delivered positive long-run rewards in a wide range of investment contexts.

Conversely, buying financial catastrophe insurance and holding speculative lottery-like investments have delivered poor long-run rewards.

The value function

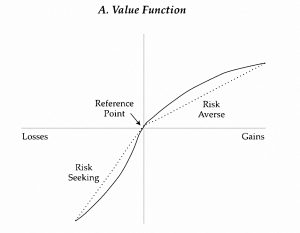
CAPM says that skewness is not priced, for two reasons:

1. Investors have a symmetrical value function,
2. And in any case, returns are normally distributed (not skewed).

In practice, investors in aggregate have a value function like the one in the chart.

• They are particularly keen on assets that will provide (relatively) high returns when markets are volatile – this is known as the coskewness with the market.

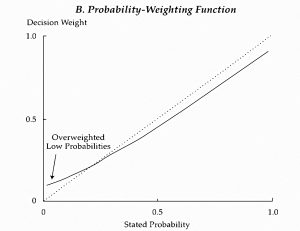
Overweighting low probability events

Kahneman and Tversky’s prospect theory explains the simultaneous demand for lottery tickets and insurance through the over-weighting of low-probability events.

• This means that people like large (but unlikely) payoffs and will buy tickets to win them, but dislike large (but unlikely) losses and will insure against them.

Taleb argues that people actually prefer regular small gains plus occasional large losses – they like negative skew.

Other research suggests that salient (vivid/recent) low probability events are over-weighted, but non-salient unlikely events (in effect, things which are thought to be impossible, or are never even considered) are under-weighted.

• This can resolve the tension between Kahneman and Taleb.

Left tail – insurance

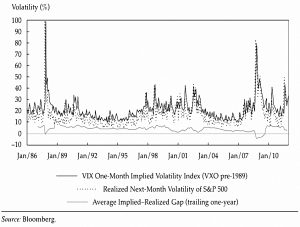
Implied (future) volatility is almost always higher than the realised volatility, particularly for equity indices.

• This gives an edge to put sellers and makes buying the VIX a losing (insurance) strategy.

Timing

Antti says that timing matters:

Low-probability events are not always overweighted, and insurance is not always overpriced.

Since salience is the driver of the over-weighting, the over-pricing should be worst just after adverse events.

• He suggests a valuation-oriented timing strategy for selling insurance (put options).

ERN’s Option Strategy

Merton Model

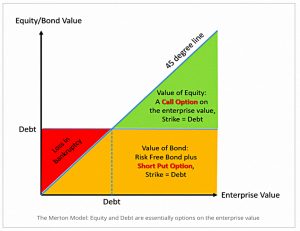
ERN begins by explaining that owning a stock is just like owning an option on the firm, with a strike price equal to the value of the firm’s debt.

• Bondholders only lose money when the value of the firm falls below the debt load.

At that point, equity holders are wiped out entirely.

This is not ERN’s idea – it’s the Merton model, named after Nobel prize-winner Robert Merton.

Lego blocks

ERN also uses Lego blocks to explain how options work.

1. The first two columns show that the return on a stock index is the same as that on cash plus an index future.
2. Column three shows that bonds plus index futures would produce an even higher return, whilst adding diversification.
   • Note that this is under normal conditions – bond yields are now so low they don’t really beat cash for private investors, and they have additional risks.
3. Column four uses lower-yielding Muni bonds, which have tax advantages in the US.
   • ERN has also leveraged up the equity future to overcome the tax on that.
4. Column five shows the after-tax return is higher than the pre-tax return of the stocks in column one.
   • Plus the bonds mean that volatility is lower, and the combined column has an imperfect correlation with stocks.

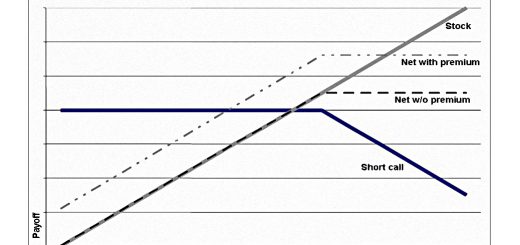
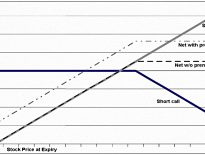
Covered calls

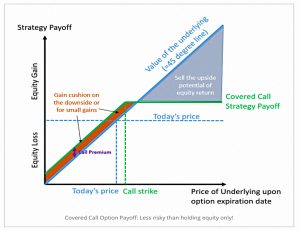
ERN uses the covered call option strategy to show that options don’t need to be risky.

• Here you own the underlying stock and sell a call on it, sacrificing any large upside.

The risk is lower than for just holding the stock, as you benefit from the sale premium when the stock goes down or has small gains.

Like ERN’s strategy of writing puts, selling covered calls returns the same as the S&P but with lower volatility.

ERN says that selling “excess” upside is well suited to those who have already reached FI.

Brokers

ERN points out that regular brokerage firms charge a lot to trade options (and options on futures, which is what ERN trades).

• He recommends that you use a specialist, like Interactive Brokers.

He says that the annual charges on a long equities futures contract are around 0.03%, which is cheaper than the best ETFs.

Avoiding the downside

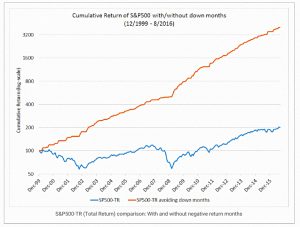
From 2000 to 2016, the S&P 500 (actually the SPY ETF) returned 4.3% pa.

• If you remove all the down months, the return leaps to 24.8% pa.

Of course, that’s easier said than done.

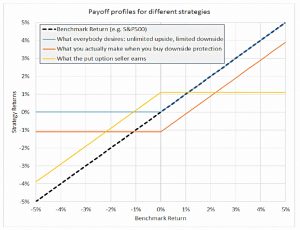
In the chart, the 45-degree line is the benchmark (SPY).

• The blue line is the return profile we want (all upside, no downside).
• The orange line is what you get when you BUY a put option.
  • This is the blue line shifted down by the premium you paid.
• The yellow line is what the SELLER of the put option gets.

The problem with buying the puts, as we’ve already alluded to, is that they are too expensive.

• The potential gain is around 20% pa, but the cost of the puts is around 16% pa in a normal (quiet) month.

And when things get jumpy, the cost leaps to somewhere between 30% pa and 80% pa.

Short puts

So instead, ERN takes the opposite side of the trade – he sells puts.

• This is the yellow line on the chart, with unlimited downside and limited upside.

Since no-one wants that kind of profile, it is underpriced and has good returns.

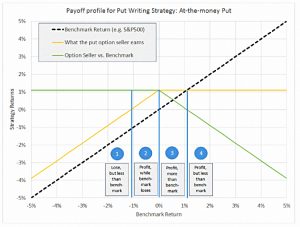
ERN argues that the return profile for writing at-the-money (ATM) puts is not that bad.

The chart shows the benchmark and the yellow line as before, with the difference between them shown as the green line.

• In zone 1, you lose less than the benchmark
• In zone 2, you win while the benchmark loses
• In zone 3, you win more than the benchmark
• In zone 4, you underperform the benchmark, but you still make a profit

This strategy outperforms the S&P with lower volatility.

Conclusions

We’ll leave it there for today – here’s what we’ve’ covered:

1. People have an aversion to negative skew, which means that they overpay for insurance and lottery tickets.
2. This seems to be related to the over-weighting of salient but unlikely events (which does not contradict Taleb’s assertion that we underweight “impossible” events.
3. So selling insurance and/or lottery tickets can be profitable.
4. Selling insurance (writing options) is the easier of these two strategies for private investors to implement.
5. Options are not as complicated or (necessarily) as risky as most people imagine.
6. ERN successfully uses a strategy of selling ATM index puts in large size.

In the next article, we’ll look at ERN’s strategy in more detail.

• Until next time.