Klement on Portfolio Construction

Today’s post looks at an old paper on portfolio construction by Joachim Klement.

Joachim Klement

Regular readers will be familiar with the Quick Links section in my Weekly Roundup posts.

• This links to the articles I have posted that week on Reddit and Twitter.

In recent weeks, I’ve been posting a lot of links from Joachim Klement’s blog, which has the tag line:

Thoughts on financial markets by a grumpy, middle-aged German. What more could you want.

Here’s an extract from his bio:

Joachim Klement is an investment strategist based in London. Throughout his professional career, Joachim focused on asset allocation, economics, equities and alternative investments.

During his career in the financial services industry, Joachim worked as investment strategist in a Swiss private bank and as Chief Investment Officer for Wellershoff & Partners, an independent consulting company for family offices and institutional investors.

Joachim blogs several times a week, and I recommend that you subscribe.

This week he mentioned an old paper of his on Portfolio Construction, so I thought I would take a look.

• It’s from 2006 and written for UBS (where I also used to work).

I wouldn’t normally look at a paper this old, but it’s from a writer I admire on a topic that I’m very interested in, so I’ve made an exception.

Portfolio Construction

The idea of the paper is that mean-variance optimisation – MVO, which forms the basis of many people’s approach to portfolio optimisation, including my own – can be invalidated by errors in the estimates of future returns, variances and correlations.

• The MVO process is very sensitive to the inputs.

To counteract this, I use long-run data for historical variances and co-variances.

• I then assume that future risk-adjusted returns for all assets are the same (that they all have the same Sharpe Ratio).

Joachim looks at three methods for dealing with parameter uncertainty:

1. Portfolio resampling
2. Bayesian estimation
3. Equal weighting

The hand-crafting approach I use (the name comes from Robert Carver, but I was using a similar approach before I read his book) incorporates equal-weighting within groups of similar assets.

• As Joachim points out, equal weighting assumes no knowledge of the future, which maps well to my equal SR approach.

All of Joachim’s methods outperform “traditional” MVO and he recommends that some combination of them be followed.

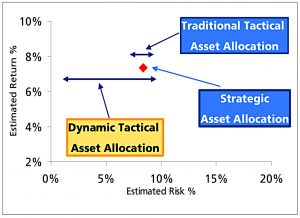
Tactical asset allocation

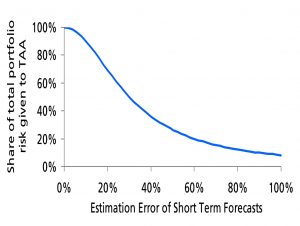
Joachim also looks at active (tactical) asset allocation using near-term forecasts (which should have smaller estimation errors than long-term forecasts).

• This leads him to recommend a 50% allocation to tactical assets.

This number is one that I have found hard to pin down, with previous estimates ranging from 10% to 40%.

• I currently have 11% of my net worth allocated tactically (equal to 22% of my listed portfolio).

So I will need to think about whether to move that number higher.

Baseline

All portfolios have constraints and for his case study Joachim chooses an international equity portfolio based on eight geographies:

• US, UK, France, Germany, Switzerland, Japan, Hong Kong and Australia.
• For historical returns, he uses the monthly returns of the respective MSCI total return indices over 30 years, from June 1976 to June 2006.

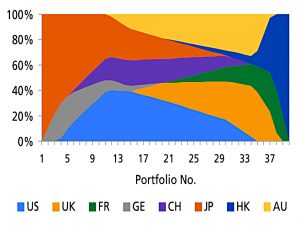
The chart shows the composition of 40 portfolios from lowest return (all JP) to highest (all HK).

• Most of the portfolios are concentrated in a few markets, and the relative proportions change rapidly.

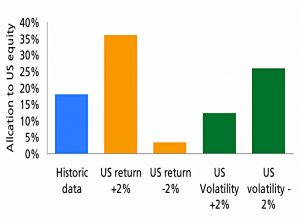
This chart shows how changes in return and volatility can greatly affect allocations (in this example, to the US).

• MVO overweights high return, low volatility assets, and errors in these estimates will have a big impact.

This – and the failure of Long Term Capital Management – is why MVO has such a bad reputation.

Resampling

The baseline portfolio is built from an efficient frontier based on historical data.

• The first alternative approach taken by Joachim is to resample 500 five-year histories by randomly selecting 60 months from the 300 in the data.

This is a Monte Carlo approach.

• I don’t support the use of Monte Carlo in equity markets because it ignores sequential effects.
• In equity markets in particular – but also in others – crashes tend to be followed by sharp recoveries.

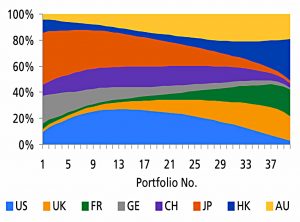
Resampling does lead to more stable and diversified portfolios.

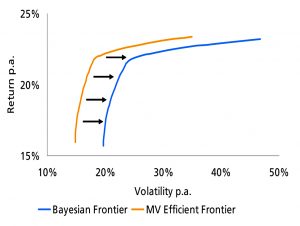
Bayesian Efficient Frontiers

Joachim calls the next approach Bayesian shrinkage of the input covariance matrix.

Bayesian statistics offers a mathematical way to incorporate estimation errors into the estimated covariance matrix and/or the estimated return vector.

As an example, consider an asset with 8% return and 15% variance.

• If the estimation error on the return is 30%, then the risk parameter would be increased to 22.5% ([30% + 15%] / 2).

The efficient frontier shifts to a higher risk level, with returns unchanged.

• The higher the estimation errors, the closer we approach my preferred solution of equal SRs.

Equal weighting

To test the approaches, Joachim splits the sample:

• The first 15 years is the input data.
• The second 15 years is used to test portfolio returns.

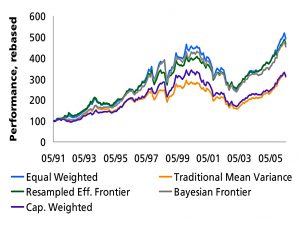
He uses five portfolios:

1. Traditional MVO
2. Resampled efficient frontier (five-year window)
3. The Bayesian efficient frontier (using a 50% estimation error)
4. Market capitalization-weighted (MSCI World)
5. Naïve 1/N allocation (equal weights)

I like these results:

• Market cap and traditional MVO do much worse than the other approaches
• Equal weight is best of all

Near-term forecasts

Joachim points out that near-term (one-year) forecasts should be better than long-term ones.

• A reasonable error of 30% would lead to a 50% tactical allocation within a portfolio.

The standard tactical allocation at the time the paper was written was 10% (close to my own tactical allocation).

• Of course, I’m not making active long-term return estimates (I use equal SRs instead) so it’s not a direct comparison.

Conclusion

I’ve really enjoyed working through this paper:

• It’s short and very readable
• It analyses an area of great importance to private investors, and
• It has actionable takeaways (even if they are to stick with what I’m already doing).

Jochim’s final words are:

A pragmatic approach could be to calculate efficient portfolios using traditional Markowitz mean variance optimization  and then “mix” it with the naïve [equal weight] portfolio to achieve better diversification.

Which is basically what I do.

• Until next time.